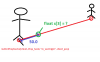
Найти точку в 50.0 единицах от игрока по отношению к другому игроку (рисунок прилагаю)

[Banana]

Здравствуйте, помогите пожалуйста найти float X[3]

 

[Boeing 767]

Из координаты второго игрока вычитаешь координаты первого, получаешь вектор(нужное направление) умножаешь его на 50 или сколько тебе надо. Потом просто к координате первого добавляешь тот самый вектор и получаешь нужную точку.

 

[Grey83]

Boeing 676, только между вычитанием и умножением нужно сделать нормализацию NormalizeVector · vector · SourceMod Scripting API Reference (а то ты умножишь расстояние м/у игроками в 50 раз, а не получишь вектор размером 50 единиц)

 

[Dragokas]

Вроде так (могу ошибаться):

#pragma semicolon 1
#pragma newdecls required

#include <sourcemod>
#include <sdktools>

public void OnPluginStart()
{
    RegConsoleCmd("sm_tele", Cmd_Tele);
}

Action Cmd_Tele(int client, int args)
{
    TeleportToNearest(client, -1);
    return Plugin_Handled;
}

// Телепортирует в сторону ближайшего игрока из указанной команды не дальше, чем на указанную дистанцию
//
stock bool TeleportToNearest(int client, int team, float distance = 50.0)
{
    int iNear;
    float vecOrigin[3], vecTarget[3], dir[3], endpos[3], dist;
    
    // вместо iNear можно подставить нужного клиента
    iNear = GetNearestClient(client, team);
    if (iNear == -1)
        return;
    
    GetClientAbsOrigin(client, vecOrigin);
    GetClientAbsOrigin(iNear, vecTarget);
    
    dist = GetVectorDistance(vecOrigin, vecTarget, false);
    if (dist <= distance)
    {
        TeleportEntity(client, vecTarget, NULL_VECTOR, NULL_VECTOR);
        return;
    }
    
    PrintToChat(client, "Teleport to: %N", iNear);
    
    SubtractVectors(vecTarget, vecOrigin, dir);
    NormalizeVector(dir, dir);
    ScaleVector(dir, distance);
    AddVectors(vecOrigin, dir, endpos);
    
    TeleportEntity(client, endpos, NULL_VECTOR, NULL_VECTOR);
}

// Получает ближайшего клиента из указанной команды
// @team: -1 - все команды
//
int GetNearestClient(int client, int team) {
    float tpos[3], spos[3], dist, mindist;
    int i, iNear;
    mindist = 0.0;
    iNear = -1;
    GetClientAbsOrigin(client, tpos);
    
    for (i = 1; i <= MaxClients; i++) {
        if (i != client && IsClientInGame(i) && (GetClientTeam(i) == team || (team == -1 && GetClientTeam(i) != 1)) && IsPlayerAlive(i)) {
            GetClientAbsOrigin(i, spos);
            dist = GetVectorDistance(tpos, spos, false);
            if (dist < mindist || mindist == 0.0) {
                mindist = dist;
                iNear = i;
            }
        }
    }
    return iNear;
}

 

[Grey83]

    SubtractVectors(vecTarget, vecOrigin, dir);
    NormalizeVector(dir, dir);
    ScaleVector(dir, distance);
    AddVectors(vecOrigin, dir, endpos);

Вот про выделенное я и говорил

 

[Dragokas]

Честно говоря в векторах едва ли шарю.
А можно на пальцах в двух словах или ссылкой пояснить, что именно нормализация делает?

 

[Grey83]

Dragokas, делает вектор равным 1

 

[Reiko1231]

@Dragokas, вектор направления является относительной величиной. В нём недостаточно информации, чтобы можно было сказать о чём-то другом, кроме направления. Чтобы не рассказывать линейную алгебру, сразу перейду на игровую математику.
Допустим у нас есть два игрока. Координаты первого игрока (10, 10), координаты второго (20, 15). Тогда вектор направления от первого игрока ко второму будет равен (x2-x1, y2-y1), т.е. (10, 5). А теперь посмотрим на обратную задачу - мы знаем вектор направления между двумя игроками, который равен (10, 5). Очевидно, что по этой информации мы не сможем найти нужные координаты игроков, т.к. существует бесконечное количество комбинаций векторов, чья разность будет равна (10, 5).

Теперь рассмотрим ситуацию ТС. Оставим те же координаты игроков, а значит и направляющий вектор у нас (10, 5). А мы например хотим найти точку, которая расположена на 2 единицы от первого игрока. Если мы просто умножим направляющий вектор на два, то мы получим координату, на которой расстояние между первым игроком и вторым в два раза больше текущего. А всё потому что у нас вектор направления относительная величина. Одно из полезных применений - можно легко найти точку, расположенную ровно по середине между игроками (умножаем на 0.5), точку на 10% от первого игрока (умножаем на 0.1) и т.д.
А как же тогда найти точку на две единицы от первого игрока? Вот тут приходит на помощь так называемая нормализация вектора. Это операция, которая делает модуль (длину) вектора равной единице. Делается это просто - каждая из координат вектора делится на модуль вектора. Модуль (длину) вектора посчитать легко - это теорема Пифагора - у нас есть два катета, нам нужно найти гипотенузу, которая и будет длиной вектора. Для нашего случая нормированный вектор будет (2/√5, 1/√5) (лень подбирать числа, чтобы получился не иррациональные числа). Вот как раз умножая его на 2, мы получим расстояние в две единицы от первого игрока.

Примеры с математикой для двумерных векторов, у которых координата по y будет равна 0 (одномерный случай). Тут как раз будут красивые числа.
Пусть координаты первого игрока (50, 0), второго (100, 0), третьего (200, 0). Нужно найти точку, на 20 единиц удалённую от первого игрока как для второго, так и третьего игрока. Очевидно, что искомая точка имеет координаты (70, 0) (т.к. все три игрока стоят на одной прямой).
Вектор направления 1->2 = (50,0), 1->3 = (150, 0). Теперь если мы просто умножим оба вектора на 20, то получим (1000, 0) и (3000, 0). Ясно, что это далеко не те координаты, которые мы искали. А если мы отнормируем что первый вектор, что второй, то получим (1, 0), поскольку длина вектора (50, 0) есть 50, а для (150, 0) - 150. И теперь умножая нормированный вектор на 20, мы получим (20, 0). Прибавив к начальной точке (50, 0), мы получим искомую координату (70, 0).

Тут можно почитать больше (плюс картинки) - Векторная алгебра — Документация Godot Engine latest.

 

[Dragokas]

Ооох, не рассчитывал на столь развёрнутый ответ.
Спасибо вам огромное. Очень хорошо растолковано. Наконец-то пришло понимание.
Оставлю мини-шпаргалку "для себя":
* вектор направления = разница между векторами расположения игроков.
* нормализованный вектор направления = вектор направления / длину вектора направления (можно рассчитать по теореме Пифагора).
* скалирование вектора направления = умножение вектора направления на указанную константу N:
- для нормализованного вектора направления результат = смещению на N юнитов в направлении от 1 игрока ко 2.
- для не_нормализованного вектора направления результат = смещению в N раз (дистанций между игроками 1 и 2) в направлении от 1 игрока ко 2.
Для получения абсолютной результирующей координаты, этот вектор направления нужно прибавить к исходной координате игрока.

Можно еще понаглею? Как перевернуть вектор направления, т.е. мы получили направление от 1 ко 2 игроку, как сделать чтобы оно направлялось наоборот от 2 к 1
(именно через функции). То что можно поменять местами аргументы у SubtractVectors я знаю.
NegateVector · vector · SourceMod Scripting API Reference - это не оно?

 

[Grey83]

Dragokas, оно